Quadrature

I lied again, I'm sorry. I'll try and post at least one more time during my elongated period of doing nothing. That very well could be a lie, but I'm going to try anyway.

I just got a book about famous math axioms for Christmas, and I saw something kind of cool in there. That reminded me of my promise during Thanksgiving to post, which I obviously broke. Sorry about that again.

~~~~~~~~~~

A really, really long time ago, the ancient Greeks were obsessed with geometry and number theory. This led to the idea of quadrature, the idea that for a (usually arbitrary) figure, a square could be constructed off of that figure with an area equal to it. For example, if you wanted a quadrature of a 9x4 rectangle, you would have to construct a square with side length 6. However, that's not really the point of quadrature-- you're supposed to be able to do it with an arbitrary figure.

Another thing to note is the nature of the constructions. You have to do it with only a straightedge and a compass, with no angles or lengths measurable. However, before we start, there are a lot of simple, pre-established things you can do with your two tools, so when I say "construct a midpoint" or something like that, just assume for the sake of the conversation (monologue, really) that it's possible, no questions asked. OK? OK.

~~~~~~~~~~

The first thing you need to learn is rectangles. They're pretty easy.

1. You have your arbitrary rectangle, ABCD.

2. Extend the edges from corner D to a reasonably long length.

3. Construct a circle with center D and radius CD. (The red dotted circle)

4. Mark point E where BD's extension and the circle intersect.

4. Construct F as the midpoint of BE.
5. Construct a circle with center F and radii BF and EF. (The blue dotted circle)
6. Mark point G where CD's extension and circle F intersect.
7. Construct a square with side DG. This square has the same area as ABCD.

~~~~~~~~~~~

Squaring the triangle is just building off of the rectangle.

1. Start with your arbitrary triangle, ABC.

2. Construct the altitude to point C.

3. Construct the midpoint of the altitude.

4. Construct the rectangle with height ED and base AB.

             At this point, compare on the basic formulae for the areas of a triangle and a rectangle, A=b*h/2   and    A=bh. One way to make the areas equal would haves the bases the same length and the height of the triangle be twice that of the rectangle. This is exactly what we have already constructed.

             From here you can just square the rectangle and everything's hunky-dory.

~~~~~~~~~~~~

Much more annoying is the arbitrary polygon itself.

In this case, we have ourselves a random heptagon. It doesn't look very quadrable, in my opinion. In fact, it looks like a mass of lines connected together. But wait! Look at what happens:

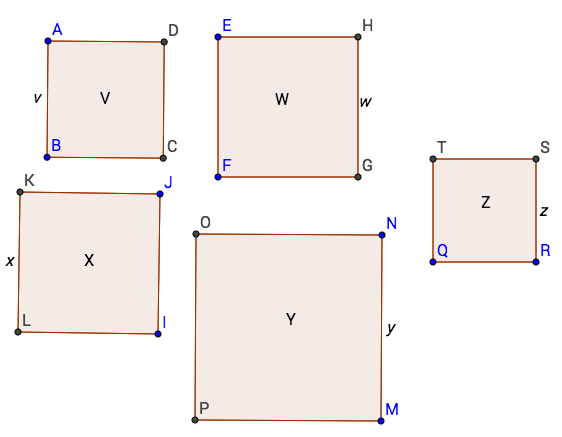
And now we have 5 triangles with areas V, W, X, Y, and Z. And we already know how to square those.

Now we have five squares with side lengths v, w, x, y, and z, the square roots of their capital letters. That's a good thing and a bad thing, because finally have a square, but too many of them. This is where we get to the interesting part.

At this point, think about the Pythagorean theorem--   a^2+b^2=c^2.

In the diagram:

w^2 + v^2 = a^2   and   a^2 + x^2 = b^2   , so

b^2 = w^2 + v^2 + x^2 = W + V + X

And:

b^2 = w^2 + v^2 + x^2   and   b^2 + y^2 = c^2  , so

c^2 = w^2 + v^2 + x^2 + y^2 = W + V + X + Y

If you don't see where this is going, then I'll explain it. Basically, by the Pythagorean theorem, a square with side length a would have and area of W+V, a square with side length b would have an area of W+V+X, and so on. Therefore, the area of a square with side length d would be equal to the sum of the areas of the smaller squares, and those are equal to the sum of the triangles, which is the area of the polygon. Neato!

~~~~~~~~~~~~

I'll continue this post tomorrow, don't worry.