Transition Matrices

These are, like, some of my favorite things in matrices, and maybe in math itself. Pay attention, yo! This is actually really useful for weather predictions, customer loyalty, and so many other things that it will blow your MIND OFF.

If you don't know yet, matrices are basically tables of data that math people use to perform operations. Happy Easter!
~~~~~~

1) Somewhere over the rainbow, there's a place with really weird weather. Let's say that:
9 rainy days out of 10 are followed by non-rainy days.
3 non-rainy days out of 10 are followed by rainy days.
By that logic, what's the chance that any particular day will be rainy?

If we try to do it the hard way, we have to use the probabilities as a result of what the previous day is and therefore the day before that, and therefore the day before THAT, and on and on until we get lost in the past and we can't really be happy anymore. But the sequence HAS to converge somewhere! I think we both can figure out right now it's possible, and I wouldn't give you a trick question about this anyway.
Speaking of the past, you're feeling slightly nostalgic for high-school math classes. One topic seems to shout out at you in particular: network matrices. You remember that you can organize a huge network of different pathways using a single matrix, with each datum representing a number of pathways from one point to another.
Being a good little nostalgic person, you decide to do this for yourself.

So there you have it. You've managed to be a clean freak. What do we do now?
Let's say we know what the weather is today. Then we also know the weather probabilities tomorrow. And, by reapplying the probability matrix again, we can figure out the day after that! The matrix squared is:
0.76   0.24
0.72   0.28
So that's the probabilities for the day after tomorrow. We can do this again and again, so where does it converge?
[M]^30=
0.75   0.25
0.75   0.25
In this case, we can assume that 30 is an artificial infinity. Referring to this new matrix, we see that after "infinity," there is a 1/4 chance of sun. Since infinity can technically count as any random day, as any operation performed on infinity is nullified, we see that the chance that any random day will be rainy is exactly 1/4. Finally!

The cool thing about these transition matrices is that you can apply them to other data.

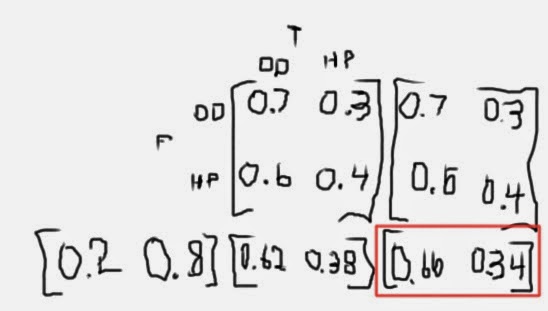
2) Two competing fast-food chains, O'Donald's and Hamburger Queen, have respective customer loyalties of 70% and 60%. If, when they open (at the same time), 80% of all customers go to Burger King, how many of the customers will go to O'Donalds after two trips?

So about 2/3 of the customers are going to O-Dees after two trips.

This repetition of matrices to find data is called a Markov Chain. Markov Chains are statistic models whose event probabilities are based on the previous event.

The matrix [(0.75, 0.25) (0.75, 0.25)] from the first problem is called a steady-state matrix, because it is the convergence of the transition matrix and cannot be altered further by the transition matrix.

Transition matrices and network matrices are used in a LOT of things: communication, business, competitions, ecology, psychology, transportation, and even biology. 

~~~~~~~~

Crazy, right? I hope you like this as much as I do.

Stay coolio

John

Infinite Series (and Sequences) (cont.) (see first post) (parentheses)

When nobody knew anything about my blog except for my friend and some German Menschen (some of my first internet traffic came via Germany, strangely enough), I had a post about infinite serieses*. I found something interesting that my math teacher recommended I put in here, and as that topic was infinite sequences, I decided to put it in here.

Here is one of the problems:
Let's make a house of cards!

Write a formula for the sequence representing the number of cards at each stage.
First method is to make a chart.
Stage-     1      2      3      4...
Cards-    2      7     15    26...
                 +5    +8   +11
Each stage increases by 3 more than the last increase. Now I'm sure there's an algebraic way to solve it from there, but my method is much more interesting.
Look at the direction that the cards face-- I marked them with lines. What's the sequence that the directions make?
Stage-   1    2    3    4
Dir 1-   1    3    6    10
Dir 2-   1    3    6    10
Dir 3-   0    1    3     6
We know those sequences! Those are triangular numbers, denoted by (y=n(n+1)/2). Because one is offset to the left, we modify the formula a bit to (y=n(n-1)/2). By definition, we can add these three formulas together to get:
y=n(3n+1)/2


Another thing we thought about in class were divergent sequences with really weird sums. For example, 1+2+3+4... is equal to -1/12, while 1+2+4+8... is equal to -1. Here's why:
For the first, imagine three sequences:
S1=1-1+1-1+1-1+1...
S2=1-2+3-4+5-6...
S=1+2+3+4+5...
Unfortunately, S1 orbits on the period of 1 and 0. So we have to use other methods. Watch this:
S1 + S1 =   1 - 1 + 1 - 1 + 1 - 1 ....
                      + 1 - 1 + 1 - 1 + 1
              =   1 + 0 + 0 + 0 + 0 + 0... = 1
So two times S1 is one, so S1 is 0.5.
And then, there's S2.
S2 + S2 =   1 - 2 + 3 - 4 + 5 - 6 + 7 ...
                      + 1 - 2 + 3 - 4 + 5 - 6 ...
              =   1 - 1 + 1 - 1 + 1 - 1 ...
Thereby establishing that S2 is 0.25.
Then watch this!
S - S2 =   1 + 2 + 3 + 4 + 5 + 6 + 7 ...
               -1 + 2 - 3  + 4 -  5 + 6 -  7
           = 4 + 8 + 12 + 16 + 20 + 24 + 28 ...
which is 4 times S. We end with:
S - 0.25 = 4S
S = -1/12
Wow! Amazing! Literally impossible!
There's probably some reason that it's not true, but who cares? It's just time to marvel at the effects of calculus on algebra!

The next one on the list (that my friend learned from a high school teacher) is
S = 1 + 2 + 4 + 8 + 16 + 32 + 64
And so we use the same method, in theory.
S - S = 1 + 2 + 4 + 8 + 16 + 32 + 64 ...
                - 1 -  2  - 4  -  8  -  16  - 32..
         = 1 + 1 + 2 + 4 + 8 + 16 + 32...
And so
S - S = S + 1
S = -1

Another impossible sum! If any people disagree they will be ridiculed forever! I'm kidding- just give me a reason that I understand.

Stay coolio,
John

PS.: This post took FOREVER

GAME THEORY

I was looking through a Barnes and Noble science section for a book on quantum theory (DON'T JUDGE), and I found a book entitled "Game Theory". I began to look through it and found it to be very interesting. Although I didn't find a good (and easy to understand) book on QT, I almost got the Game Theory.

In game theory, only two things define a game-
-there are two or more players...
-who interact to maximize a 'Utility'.

In games, Utility are the 'points'-- or, if no points, a numerical representation of the situation they're in. Usually it's an estimate.

Let's give an example.
There are two prisoners A and B. Together, they committed a crime for which they could get 10 years in prison. However, they are each offered a deal in which they can confess and testify against their partner (defect) or refuse to admit it (refuses). This is the deal to both of them:
a) If you defect and your friend refuses, you escape free and your friend gets 20 years.
b) If you both defect, you both get 5 years.
c) If you both refuse, you get 10 years.

Let's analyze!
If your friend will defect, your best option is to defect too, because it reduces your sentence by 15 years. However, if your friend will likely refuse, you should defect, as it will reduce your sentence by 10 years. Your best option is to defect, because the average between your possible sentences will reduce by 7.5 years than if you refuse. Think of it this way-

This is called a matrix, if you don't know. But I'm assuming that you do.

We could also plot it on a tree.

An interesting property of the PD is that the players technically do not interact-- it's what they do when they don't interact that makes it an interesting game.

There's a concept called Nash Equilibrium that's relatively important to game theory. From what I can tell, it's a situation where no players want to change their strategy. In a way, it means that they won't gain anything by changing their strategy.
A NE in Prisoner's Dilemma is, let's say, both players choose to defect. If either player decides to change their strategy, they'll lose.

There's also another game called Morra that you may have played. This is an interesting game that is played like rock-paper-scissors.
In Morra, only two players compete. So, on the count of whatever, each player holds up a number on their fingers from one to ten. If the sum of their numbers is even, one player wins; and vice versa.
Here's a chart I created-

Notice that the number they pick doesn't matter-– only if it's even or odd does.The odd player should do the opposite of the even player, but the even player should do the same as the odd. There is no real 'better strategy', unless you somehow read your opponent's mind, or predict the future.

Anyway, I guess that's it! There are tons of other good games-- Rock Paper Scissors, Nim, 2/3 the Average, and Fair Division (Cake Cutting). You acan look at them if you want.

Stay coolio, John

*PS: Sorry if this was a bad post-- Game Theory is extremely general*