So it's been a WHILE
I started this post in September, and I was so close to finishing it, but I obviously forgot to actually post it! I've had actually NO time to do anything since maybe September, and I'm still really tired right now because I had a competition that was a couple of hours away, and I had to do stuff, and yeah.
I'm probably going to past at least 2 more times over Thanksgiving break, so don't worry about consistency. On second thought, worry about consistency, because you know it's really bad.
Let's get into the post.
~~~~~~~~~~~~
Prove that the square root of two is irrational.
What we're going to do here is assume that the opposite is true: Sqrt(2) is rational. By that logic, Sqrt(2) can be written as the fraction (a/b), where (a) and (b) are integers. Let's also assume that the fraction is simplified to its lowest terms. If it is, then both of them can't be even-- it could be simplified more.
If (a/b)=2, then (a^2/b^2)=2. Multiplying both sides by (b^2), you get (a^2)=2(b^2). Therefore (a) is even.
Because both (a) and (b) can't be even, then proving that (b) is even would prove that Sqrt(2) is irrational.
Since a is even, we can write (a) as (2*k), where k is half of a. Therefore:
(2k)^2=2(b^2)
4(k^2)=2(b^2)
2(k^2)=(b^2)
So b is even too which proves that Sqrt(2) is irrational.
~~~~~~~~~~~~
Prove that there are an infinite amount of prime numbers.
For this one, we're going to do the same thing- assume the opposite. There 'are' a finite amount of prime numbers.
If that's true, then we can multiply all of the prime numbers together to get some number c.
However, c+1 must be prime, because every prime number would have a remainder of 1 when dividing it. So that kind of proves it wrong, and it's a relatively easy proof.
~~~~~~~~~~~~~
Stay coolio,
John
JOHN Join Coin Corn Core Coke Coke Cake Make Mate MATH Moth Mott Moot Coot Clot Clog BLOG Clog Clon Coon Coin Join JOHN
Sunday, November 23
Tuesday, September 9
Answers to the Diabolical Quiz
Did you get the answers? We'll see, I guess.
1. 144
2. 2
3. True
4. 2
5. False
6. 24
7. False
8. -12
9. True
10. -16
Believe me, there IS a way to solve this quiz. I just don't want to type it all.
Stay coolio,
John
~~~~~~~~~~~~~
PS- These are the answers to the quiz I posted last month. I'm really sorry that I haven't posted, but it's been a looooooooong couple of weeks for me. I will post tomorrow (or Thursday?), but I don't know. I have a lot of work to do, and I have to make this second on my list of priorities. But I promise I will post sometime this week. Thanks!
1. 144
2. 2
3. True
4. 2
5. False
6. 24
7. False
8. -12
9. True
10. -16
Believe me, there IS a way to solve this quiz. I just don't want to type it all.
Stay coolio,
John
~~~~~~~~~~~~~
PS- These are the answers to the quiz I posted last month. I'm really sorry that I haven't posted, but it's been a looooooooong couple of weeks for me. I will post tomorrow (or Thursday?), but I don't know. I have a lot of work to do, and I have to make this second on my list of priorities. But I promise I will post sometime this week. Thanks!
Monday, August 11
Diabolical Quiz About this Quiz
Time for another Problems w/John!!!!!!!!! You will hate me after this set.
1. What is the sum of all of the numerical answers of this quiz, including this one?
2. How many of these answers are "true"?
3. True or false: Question 1 has the highest numerical answer of this quiz.
4. How many answers are the same as this one, including this one?
5. True or false: All of the numerical answers are positive.
6. What is the average of all the numbers in this quiz, including this one?
7. True or false: The answer to Question 4 is greater than Question 2.
8. What is Question 1's answer divided by Question 8's?
9. True or false: The answer to question 6 is equal to the difference between answers 2 and 4, minus the product of answers 8 and 4.
10. What is the answer to this godforsaken question?
I'll put up answers on Wednesday.
Sorry I couldn't post last week, I was in Europe (land of the bad Internet). But honestly, not complaining.
Stay coolio,
John
1. What is the sum of all of the numerical answers of this quiz, including this one?
2. How many of these answers are "true"?
3. True or false: Question 1 has the highest numerical answer of this quiz.
4. How many answers are the same as this one, including this one?
5. True or false: All of the numerical answers are positive.
6. What is the average of all the numbers in this quiz, including this one?
7. True or false: The answer to Question 4 is greater than Question 2.
8. What is Question 1's answer divided by Question 8's?
9. True or false: The answer to question 6 is equal to the difference between answers 2 and 4, minus the product of answers 8 and 4.
10. What is the answer to this godforsaken question?
I'll put up answers on Wednesday.
Sorry I couldn't post last week, I was in Europe (land of the bad Internet). But honestly, not complaining.
Stay coolio,
John
Saturday, July 26
Hangman
Hey!
Imagine a man is convicted of murder and is sentenced to death one Saturday. The judge states that the man will be hanged sometime the next week, but the date will be a surprise-- the man won't know what day he is hanged until the noon of that day.
When the prisoner returns to his cell, he is ecstatic. Think about it: it can't be on a Saturday, because it is the last day of the week that he could be hanged on and therefore not a surprise. And if it was on Friday, he could be sure it was that day because Saturday has already been ruled out and therefore makes Friday the last possible day. So on and so forth until no day can he be hanged.
However, on Thursday, he is informed that he will be hanged. This comes as a complete surprise to him, contrary to his logic.
Consider this carefully. Is it a true paradox?
~~~~~~~~~~~~
Sorry for the short post. I'll put up an answer sometime next week, along with another post. Honestly, it's been a bit hard to do the blog, mainly because I get one hour every day to use my computer-- including free time, a research project that I have to do, and the blog.
I'll get you next week!
Stay coolio,
John
NEXT WEEK: Something Different
Imagine a man is convicted of murder and is sentenced to death one Saturday. The judge states that the man will be hanged sometime the next week, but the date will be a surprise-- the man won't know what day he is hanged until the noon of that day.
When the prisoner returns to his cell, he is ecstatic. Think about it: it can't be on a Saturday, because it is the last day of the week that he could be hanged on and therefore not a surprise. And if it was on Friday, he could be sure it was that day because Saturday has already been ruled out and therefore makes Friday the last possible day. So on and so forth until no day can he be hanged.
However, on Thursday, he is informed that he will be hanged. This comes as a complete surprise to him, contrary to his logic.
Consider this carefully. Is it a true paradox?
~~~~~~~~~~~~
Sorry for the short post. I'll put up an answer sometime next week, along with another post. Honestly, it's been a bit hard to do the blog, mainly because I get one hour every day to use my computer-- including free time, a research project that I have to do, and the blog.
I'll get you next week!
Stay coolio,
John
NEXT WEEK: Something Different
Friday, July 18
Ramsey Theory
Consider this problem:
Let's say that there are some people in a room for which some of them know each other and others do not. How many people must there be to make sure that either 3 of them are strangers to each other, or 3 have all met each other?
Another way to consider this problem is:
There are some points in a space, each connected by line segments to all of the other points. If each segment is either blue or red, then how many points must there be to ensure that there is one full triangle (with vertices on the points) outlined by all blue or all red?
In theory, these problems are exactly the same. The points are obviously people, and the color of the lines represents whether they know each other. If one color forms a triangle, three people either know each other or are total strangers to one another. Simple, right?
Anyway, the answer is 6 people. This is called the Ramsey number for two-colored triangles, written as:
R(3,3)=6
Let's call a complete graph (where all points are connected) with n points Kn. For Ramsey notation, the number of values in the parentheses represent the number of colors; the values themselves signify the graphs that we're trying to force. So R(3,6)=18 would be two colored, either forcing a red triangle or a blue K6.
Here are the Ramsey numbers that we know for now:
3, 3 = 6
3, 3, 3 = 17
3, 4 = 9
3, 5 = 14
4, 4 = 18
3, 6 = 18
3, 7 = 23
3, 8 = 28
3, 9 = 36
4, 5 = 25
6, 7 = 298
But then there are the irregular graphs, like straight lines and bowties and things like that. Well, thank you, Stefan Burr!
Let's say that there are some people in a room for which some of them know each other and others do not. How many people must there be to make sure that either 3 of them are strangers to each other, or 3 have all met each other?
Another way to consider this problem is:
There are some points in a space, each connected by line segments to all of the other points. If each segment is either blue or red, then how many points must there be to ensure that there is one full triangle (with vertices on the points) outlined by all blue or all red?
In theory, these problems are exactly the same. The points are obviously people, and the color of the lines represents whether they know each other. If one color forms a triangle, three people either know each other or are total strangers to one another. Simple, right?
Anyway, the answer is 6 people. This is called the Ramsey number for two-colored triangles, written as:
R(3,3)=6
Let's call a complete graph (where all points are connected) with n points Kn. For Ramsey notation, the number of values in the parentheses represent the number of colors; the values themselves signify the graphs that we're trying to force. So R(3,6)=18 would be two colored, either forcing a red triangle or a blue K6.
Here are the Ramsey numbers that we know for now:
3, 3 = 6
3, 3, 3 = 17
3, 4 = 9
3, 5 = 14
4, 4 = 18
3, 6 = 18
3, 7 = 23
3, 8 = 28
3, 9 = 36
4, 5 = 25
6, 7 = 298
But then there are the irregular graphs, like straight lines and bowties and things like that. Well, thank you, Stefan Burr!
Sunday, July 13
Crafts Time (cont.)
Sorry, I just want to make a note on the last post I made, about the matchbox computer.
~~~~~~~~~~
Once upon a time, there was a guy named Donald Michie. When he was in WWII, he wanted to take Japanese and go fight on the Pacific front. Naturally, however, the class was full, and he did not sign up in time. However, he was not fazed in his war effort! He was recruited to help solve the enigmatic messages of the German army, and found that he was a natural in computer analysis. He began to work harder towards the study of artificial intelligence.
Within 20 years later, he invented the tic-tac-toe MENACE. MENACE was the Matchbox Educable Naughts And Crosses Engine, one of the first perfect-able robots to play the game of tic tac toe. He made the machine by diagramming all of the possible board states on 304 separate matchboxes. Although there are 19,683 possible board layouts*, Michie reduced this number to 304 by taking rotations, mirror images, and winning positions into account, thus reducing the number by over 98%.
*If you think about it, each of the 9 squares can be in one of three states: blank, X, or O. 3^9=19683.
~~~~~~~~~~~~
Stay coolio,
John
~~~~~~~~~~
Once upon a time, there was a guy named Donald Michie. When he was in WWII, he wanted to take Japanese and go fight on the Pacific front. Naturally, however, the class was full, and he did not sign up in time. However, he was not fazed in his war effort! He was recruited to help solve the enigmatic messages of the German army, and found that he was a natural in computer analysis. He began to work harder towards the study of artificial intelligence.
Within 20 years later, he invented the tic-tac-toe MENACE. MENACE was the Matchbox Educable Naughts And Crosses Engine, one of the first perfect-able robots to play the game of tic tac toe. He made the machine by diagramming all of the possible board states on 304 separate matchboxes. Although there are 19,683 possible board layouts*, Michie reduced this number to 304 by taking rotations, mirror images, and winning positions into account, thus reducing the number by over 98%.
*If you think about it, each of the 9 squares can be in one of three states: blank, X, or O. 3^9=19683.
~~~~~~~~~~~~
Stay coolio,
John
Tuesday, July 8
Crafts Time
IT'S FUN DAY MONDAY OMG SO EXCITED!!!!!!!
So I've been at the beach for 4 days now, and that of course means a lot of reading for those less inclined to enter the water. And so I learned something new:
~~~~~~~~~
How to Make a Hexapawn Educable Robot (HER)
Materials:
1) 24 Matchboxes or Similar Containers (Preferably blank)
2) 3-4 Bags of M&Ms
3) Paper
4) 4 Colored Sharpies (Orange, Blue, Green, Red, Brown, and/or Yellow)
5) 3 Pennies (or other coins)
6) 3 Dimes (or other coins)
Procedure:
1) Copy these diagrams onto the matchboxes:
2) On each of the diagrams, color all the arrows in each diagram differently.
3) Open the bags of M&Ms and sort them by color.
4) Eat the two colors of M&Ms whose corresponding Sharpie you do not have. For example, if you don't have a yellow or brown Sharpie, eat all the yellow and brown M&Ms.
5) Put an M&M in each box for the number and color of the arrows on it. For example, if there is a
red arrow on the box, put in a red M&M.
6) Draw a three-by-three grid and put the coins on opposite sides, like so:
You are now ready to face your computer in Hexapawn!
~~~~~~~~~~
How to Play Hexapawn:
Hexapawn is a one on one game that you play against HER in order to teach it how to win! To win, you must either:
1) Capture all of your opponent's pawns,
2) Get one of your pawns to the opposite side, or
3) Be the last player to be able to move.
Your pawns move the same way that they would in chess-- they can only move forward, except they must capture diagonally-- except there are no double moves and en-passants. Good luck!
~~~~~~~~~~
How to Operate your HER:
First, arrange the matchboxes as shown in the diagram above. This makes the game run smoother.
Then you can start the game. You make your move first.
Here's how you operate the robot:
1) Find the matchbox whose diagram is either the same as the current board position or a mirror image.
2) Shake the matchbox to mix the M&Ms.
3) With your eyes closed, open the matchbox and pick a random M&M.
4) Place the M&M on top of the matchbox and observe the color of the M&M.
5) Find the corresponding arrow for the color of the M&M.
6) Make the move as indicated by the arrow.
3.5*) If there are no M&Ms in the box, the robot automatically loses.
The education of the robot is based on a reward/punishment system. When the robot wins the game, the M&Ms that are on top of the boxes are placed back inside. When it loses, take away the M&M that represents the last move that the robot made; *if a box is empty, the HER loses and you take away the M&M on last move's box.
~~~~~~~~~~
How the HER Works
Imagine a huge probability tree that represents the outcomes of each game. Each splitting of branches represents the robot's decision-- and so the end of a branch is either a win or a loss for the robot. When you remove M&Ms, you are, in essence, cutting off the branches in which the robot loses. The robot has a big advantage by going second, and so it will eventually have the ability to win every game it plays.
~~~~~~~~~~~
Stay coolio,
John
NEXT WEEK: Ramsey Numbers
Tuesday, July 1
Hailstones (The Collatz Conjecture)
Hey guys, I'm back from camp with a TON of new ideas. I got a bunch of math books as a graduation present (which would be a really mean present if I wasn't myself), and I got some new topics to discuss.
~~~~~~~~~~
In the science of the hydrosphere, we all know that water molecules present in air all eventually return to the Earth in the form of precipitation. One of the forms thereof is hail, which forms in heavy storms when liquid rain freezes onto snow pellets and begins to form solid lumps.
Let's say that layers of the atmosphere are marked by numbers, starting with one as the ground. The goal of a hailstone is, obviously to reach one.
The process that determines the path of a hailstone is this:
1) If a hailstone reaches level n, and n is odd, then the hailstone is caught by a gust of wind and shoots up to level 3n+1.
2) If n is even, then there is no wind and the hailstone falls to n/2.
3) This process is continued upon itself until n reaches 1.
For any positive integer from which the hailstone (n) begins, does n reach 1?
This can also be stated as:
~~~~~~~~~~
~~~~~~~~~~
In the science of the hydrosphere, we all know that water molecules present in air all eventually return to the Earth in the form of precipitation. One of the forms thereof is hail, which forms in heavy storms when liquid rain freezes onto snow pellets and begins to form solid lumps.
Let's say that layers of the atmosphere are marked by numbers, starting with one as the ground. The goal of a hailstone is, obviously to reach one.
The process that determines the path of a hailstone is this:
1) If a hailstone reaches level n, and n is odd, then the hailstone is caught by a gust of wind and shoots up to level 3n+1.
2) If n is even, then there is no wind and the hailstone falls to n/2.
3) This process is continued upon itself until n reaches 1.
For any positive integer from which the hailstone (n) begins, does n reach 1?
This can also be stated as:
~~~~~~~~~~
FACTS:
1. The sequence always ends [...] 16, 8, 4, 2, 1.
2. The conjecture has been proved up to about 5476377146882523136.
3. The sequence always returns to one if n is a power of 2.
4. The recurrence is undecidable (it cannot be solved by an algorithm).
5. Once the hailstone reaches 16, the hailstone is set into an infinite loop around (4,2,1).
6. Most diagrams are created in reverse.
Up to 20 iterations. Ends with one in the center.
~~~~~~~~~~~~~
Hey guys! It's good to be back. From now on, I'm going to try to have one post every Monday. I have so much to talk about, but I don't want to waste all of my ideas now! We'll see what happens later, I guess.
Stay coolio,
John
NEXT WEEK: More on Game Theory
Thursday, May 29
Illustrated Multiplication! (AKA Educational Satire)
Ever had trouble multiplying fast? Do you just want to doodle in math class? We can help you!
Try out our new product, Illustrated Math! It's easy as 'pi' and we'd LOVE to give it to you for free!
Here's a song to celebrate your discovery of this easy new trick!
How unnecessary was that?! But as an infomercial, we need some cheesy background music!
It's EASY!
Let's do a demo!
Let's multiply 51 and 23. First, we draw lines representing digits.
Great! Now let's separate the columns and count up the number of intersections in each column!
Fantastic! All we have to do is add it up!
+ 3
+ 1 7
+ 1 0
= 1 1 7 3
Let's check to see if our answer is correct!
Wow! Shazam! Fantabulous!
It's FAST!
Studies show that this new, cool multiplication trick can save you –50% time when compared against regular multiplying! This is mainly because some idiot wrote the answer on the paper during the first of the regular trials and we didn't bother to replace it!
It's CHEAP!
Even though this is more of a concept than a product, we can give it to you for free!* (This doesn't include the $19.99 shipping and handling, the complimentary $199.99 gift pack we'll send you, or the medical bill you'll need to pay after using this product! Don't read the subtext!)
It WORKS!
By the FOIL method straight from middle school algebra! We can't believe you didn't figure this out yourselves, you disgraces to all humanity! (Even though we didn't figure it out either. Shh, don't tell)
And it's probably harmless!
The 2% of subjects that survived reported that it had really changed their lives for better or worse! You don't want to know which!
CALL 1-800-I-SEE-U-PN to order NOW!
Make checks payable to Bad Products Inc. ©.
*Batteries, Medical Consultation, and Michael Jackson not included.
The more common and l side effects may include Stockholm Syndrome, Bruce Jenner approximation syndrome, organ inversion, and zombification. At the risk of getting sued we can't tell you the nastier ones or you wouldn't buy this product.
~~~~~~~~~~
Hey everybody! I'm BACK! Sorry for not posting-- I've had a nice little month of studying for exams. I actually finished a post two weeks ago and, of course, the school server was shut down and it didn't work. I'm going to post that next week to make up for a), my long absence from your world, and b), the nastiness of this post.
Sorry for not posting earlier, but April Showers bring the overpowering stench of May exams!
Stay coolio,
John
IMPORTANT NOTE- Tragically, I'm not going to be able to post very much this summer, because it's summer. I promise I'll get back to you in late June or early July!
~~~~~~~~~~
Hey everybody! I'm BACK! Sorry for not posting-- I've had a nice little month of studying for exams. I actually finished a post two weeks ago and, of course, the school server was shut down and it didn't work. I'm going to post that next week to make up for a), my long absence from your world, and b), the nastiness of this post.
Sorry for not posting earlier, but April Showers bring the overpowering stench of May exams!
Stay coolio,
John
IMPORTANT NOTE- Tragically, I'm not going to be able to post very much this summer, because it's summer. I promise I'll get back to you in late June or early July!
Wednesday, May 7
Probs of the Week v. 3.0
Yep. It's back.
1. Based on the following facts:
ab=1
b+c=0
b+c+d=0
bc=-9
c+a<d
What is a+b?
2. The first term of a geometric sequence is 12. If the geometric mean of the first 3 terms is 18, what's the third?
3. If three competing products have loyalties of 20%, 60%, and 80%, and half of the customers that switch go to one of the other products, then how many customers will go to each after they begin marketing regularly?
4. How many distinct integers are in the set of differences between numbers of the set, {1,3,5,7,9,10, 11,13}?
5. How much wood could a woodchuck chuck if a woodchuck could chuck wood?
~~~~~~~~~~~~~
1. Let's gather our info:
a) a is the reciprocal of b, and the negative reciprocal of c
b) b is equal to negative c, and their product is -9
c) d is equal to 0, and is greater than the sum of a and c.
We can draw the conclusion that:
d) b and c are equal to 3 and -3, in some order
e) a is equal to either -1/3 or 1/3
f) a+c=-3+(1/3)<0
g) a=1/3, b=3, c=-3
h) a+b=3+(1/3)=10/3
2. By definition, the geometric mean is the second term. The ratio of 18 to 12 is 3/2; 3/2 times 18 is 27.
3. The matrix is...
[ 0.2 0.4 0.4]
[ 0.2 0.6 0.2]
[ 0.1 0.1 0.8]
To the power of 30 it reaches
[ 0.1429 0.2857 0.5714]
[ 0.1429 0.2857 0.5714]
[ 0.1429 0.2857 0.5714]
4. Let's remove the 10 for now. The differences between the numbers are the even integers from 2 to 12-- that makes 6. Now, the 10 is different- the difference between it and the other numbers is always odd, from one to nine. Six plus five, if you couldn't figure out, is 11.
5. Enough to spray splinters into your tongue... who really cares? According to a website I found, the answer is 22 cubic inches. That's more of a biology problem anyway.
So YEAH!
Bye sweet children!
John
PS: We're learning about conditionals and logic problems in class today, and it's taking absurdly long for some of my friends to figure it out. Oh, sweet rationale... where have you run off to now?
1. Based on the following facts:
ab=1
b+c=0
b+c+d=0
bc=-9
c+a<d
What is a+b?
2. The first term of a geometric sequence is 12. If the geometric mean of the first 3 terms is 18, what's the third?
3. If three competing products have loyalties of 20%, 60%, and 80%, and half of the customers that switch go to one of the other products, then how many customers will go to each after they begin marketing regularly?
4. How many distinct integers are in the set of differences between numbers of the set, {1,3,5,7,9,10, 11,13}?
5. How much wood could a woodchuck chuck if a woodchuck could chuck wood?
~~~~~~~~~~~~~
1. Let's gather our info:
a) a is the reciprocal of b, and the negative reciprocal of c
b) b is equal to negative c, and their product is -9
c) d is equal to 0, and is greater than the sum of a and c.
We can draw the conclusion that:
d) b and c are equal to 3 and -3, in some order
e) a is equal to either -1/3 or 1/3
f) a+c=-3+(1/3)<0
g) a=1/3, b=3, c=-3
h) a+b=3+(1/3)=10/3
2. By definition, the geometric mean is the second term. The ratio of 18 to 12 is 3/2; 3/2 times 18 is 27.
3. The matrix is...
[ 0.2 0.4 0.4]
[ 0.2 0.6 0.2]
[ 0.1 0.1 0.8]
To the power of 30 it reaches
[ 0.1429 0.2857 0.5714]
[ 0.1429 0.2857 0.5714]
[ 0.1429 0.2857 0.5714]
4. Let's remove the 10 for now. The differences between the numbers are the even integers from 2 to 12-- that makes 6. Now, the 10 is different- the difference between it and the other numbers is always odd, from one to nine. Six plus five, if you couldn't figure out, is 11.
5. Enough to spray splinters into your tongue... who really cares? According to a website I found, the answer is 22 cubic inches. That's more of a biology problem anyway.
So YEAH!
Bye sweet children!
John
PS: We're learning about conditionals and logic problems in class today, and it's taking absurdly long for some of my friends to figure it out. Oh, sweet rationale... where have you run off to now?
Tuesday, May 6
Science Blog- Friend of the Devil is a Friend of Mine
Go follow this guy!
Ben's Science Blog
For updates and interesting posts on astronomy, physics, geology, and every other science topic you could ever imagine, just consult this blog. He posts almost regularly, so he'll really keep you occupied with his mind-blowing facts.
~~~~~~~~~
This is just a quick update- he did me a favor so I did him one in return. Sha-zam!
Ben's Science Blog
For updates and interesting posts on astronomy, physics, geology, and every other science topic you could ever imagine, just consult this blog. He posts almost regularly, so he'll really keep you occupied with his mind-blowing facts.
~~~~~~~~~
This is just a quick update- he did me a favor so I did him one in return. Sha-zam!
Monday, May 5
Double-Dog-Derivatives
What happens when the derivative of a function is itself?
As you may already know, a derivative is just a fancy little term for slopes of tangent lines. Or slopes of points, for people who view it differently. Anyway...
There are certain functions whose derivative is itself. What are some of these?
~~~~~~~~~
"e^x" is the only exponential function that has this property. This is just one of the many amazing applications of Euler's number.
"0" is another, but anybody could figure that one out.
"sin(x)" and "cos(x)" have their derivatives every fourth time.
"cosh(x)" and "sinh(x)" also have their own derivatives.
Just a note-- for "log x", the second derivative approaches the original when the base approaches infinity.
No polynomial function works, according to this theorem:
For any polynomial function "f(x)=c*x^n", its derivative is "c*n*x^(n-1)". So even if the coefficient is the same, the degree is offset by one.
~~~~~~~~~~
Sorry for the short post. I started the post, then kind of realized that I didn't really have much to work with...
Hang in there, people! I have final exams coming up, so I might not post much. Just wait, OK?
Stay coolio,
John
As you may already know, a derivative is just a fancy little term for slopes of tangent lines. Or slopes of points, for people who view it differently. Anyway...
There are certain functions whose derivative is itself. What are some of these?
~~~~~~~~~
"e^x" is the only exponential function that has this property. This is just one of the many amazing applications of Euler's number.
"0" is another, but anybody could figure that one out.
"sin(x)" and "cos(x)" have their derivatives every fourth time.
"cosh(x)" and "sinh(x)" also have their own derivatives.
Just a note-- for "log x", the second derivative approaches the original when the base approaches infinity.
No polynomial function works, according to this theorem:
For any polynomial function "f(x)=c*x^n", its derivative is "c*n*x^(n-1)". So even if the coefficient is the same, the degree is offset by one.
~~~~~~~~~~
Sorry for the short post. I started the post, then kind of realized that I didn't really have much to work with...
Hang in there, people! I have final exams coming up, so I might not post much. Just wait, OK?
Stay coolio,
John
Saturday, May 3
The Prime Test
A while ago, some famous math guys came up with a new theorem to test for primes. That is, you can use this test to find out if any number is prime. The test is much better to use with smaller numbers, because the bigger a number, the longer it takes to run this test.
By the way, I saw this on a Youtube video, but I noticed a pattern a while ago related to this.
~~~~~~~~~~
Let's go back to Pascal's Triangle. Pascal's Triangle is a sort of array of numbers starting at one at the top, and each number is the sum of the two numbers above it. It looks like this:
By the way, I saw this on a Youtube video, but I noticed a pattern a while ago related to this.
~~~~~~~~~~
Let's go back to Pascal's Triangle. Pascal's Triangle is a sort of array of numbers starting at one at the top, and each number is the sum of the two numbers above it. It looks like this:
Now take a look at the rows whose second number is prime. All of the numbers following it are divisible by it-- excluding 1. And all of the composite numbers don't have this property.
You also have probably heard of the Binomial Theorem. This theorem states that all coefficients of the expansion of:
(x+1)^n (or (a+b)^n)
are the terms of the nth row of Pascal's Triangle, which is also a cool property.
So if we combine our previous discovery and the Binomial Theorem, we can get:
"All of the coefficients of the expansion of (x+1)^n are divisible by n if and only if n is prime, excluding the coefficient one of the first and last terms."
And if we get rid of that last part and reverse that, we get:
"Any whole number n is prime if all of the coefficients of
(x+1)^n - x^n - 1
are divisible by n."
Let's try it out, hmm?
7: coefficients are 7, 21, 35, 35, 21, 7 yes
10: 10, 45, 120, 210, 252, 210, 120, 45, 10 no
It works!
I just thought that this was a really interesting breakthrough.
Sty coolio,
John
Monday, April 21
Transition Matrices
These are, like, some of my favorite things in matrices, and maybe in math itself. Pay attention, yo! This is actually really useful for weather predictions, customer loyalty, and so many other things that it will blow your MIND OFF.
If you don't know yet, matrices are basically tables of data that math people use to perform operations. Happy Easter!
~~~~~~
1) Somewhere over the rainbow, there's a place with really weird weather. Let's say that:
9 rainy days out of 10 are followed by non-rainy days.
3 non-rainy days out of 10 are followed by rainy days.
By that logic, what's the chance that any particular day will be rainy?
If we try to do it the hard way, we have to use the probabilities as a result of what the previous day is and therefore the day before that, and therefore the day before THAT, and on and on until we get lost in the past and we can't really be happy anymore. But the sequence HAS to converge somewhere! I think we both can figure out right now it's possible, and I wouldn't give you a trick question about this anyway.
Speaking of the past, you're feeling slightly nostalgic for high-school math classes. One topic seems to shout out at you in particular: network matrices. You remember that you can organize a huge network of different pathways using a single matrix, with each datum representing a number of pathways from one point to another.
Being a good little nostalgic person, you decide to do this for yourself.
So there you have it. You've managed to be a clean freak. What do we do now?
Let's say we know what the weather is today. Then we also know the weather probabilities tomorrow. And, by reapplying the probability matrix again, we can figure out the day after that! The matrix squared is:
0.76 0.24
0.72 0.28
So that's the probabilities for the day after tomorrow. We can do this again and again, so where does it converge?
[M]^30=
0.75 0.25
0.75 0.25
In this case, we can assume that 30 is an artificial infinity. Referring to this new matrix, we see that after "infinity," there is a 1/4 chance of sun. Since infinity can technically count as any random day, as any operation performed on infinity is nullified, we see that the chance that any random day will be rainy is exactly 1/4. Finally!
The cool thing about these transition matrices is that you can apply them to other data.
2) Two competing fast-food chains, O'Donald's and Hamburger Queen, have respective customer loyalties of 70% and 60%. If, when they open (at the same time), 80% of all customers go to Burger King, how many of the customers will go to O'Donalds after two trips?
If you don't know yet, matrices are basically tables of data that math people use to perform operations. Happy Easter!
~~~~~~
1) Somewhere over the rainbow, there's a place with really weird weather. Let's say that:
9 rainy days out of 10 are followed by non-rainy days.
3 non-rainy days out of 10 are followed by rainy days.
By that logic, what's the chance that any particular day will be rainy?
If we try to do it the hard way, we have to use the probabilities as a result of what the previous day is and therefore the day before that, and therefore the day before THAT, and on and on until we get lost in the past and we can't really be happy anymore. But the sequence HAS to converge somewhere! I think we both can figure out right now it's possible, and I wouldn't give you a trick question about this anyway.
Speaking of the past, you're feeling slightly nostalgic for high-school math classes. One topic seems to shout out at you in particular: network matrices. You remember that you can organize a huge network of different pathways using a single matrix, with each datum representing a number of pathways from one point to another.
Being a good little nostalgic person, you decide to do this for yourself.
So there you have it. You've managed to be a clean freak. What do we do now?
Let's say we know what the weather is today. Then we also know the weather probabilities tomorrow. And, by reapplying the probability matrix again, we can figure out the day after that! The matrix squared is:
0.76 0.24
0.72 0.28
So that's the probabilities for the day after tomorrow. We can do this again and again, so where does it converge?
[M]^30=
0.75 0.25
0.75 0.25
In this case, we can assume that 30 is an artificial infinity. Referring to this new matrix, we see that after "infinity," there is a 1/4 chance of sun. Since infinity can technically count as any random day, as any operation performed on infinity is nullified, we see that the chance that any random day will be rainy is exactly 1/4. Finally!
The cool thing about these transition matrices is that you can apply them to other data.
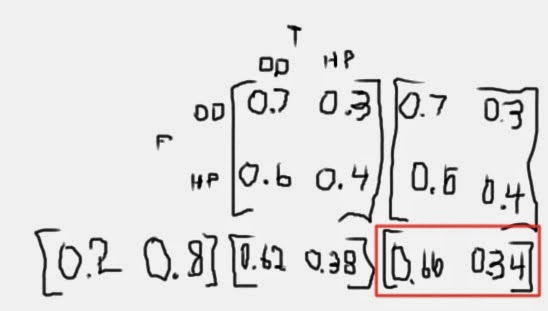
2) Two competing fast-food chains, O'Donald's and Hamburger Queen, have respective customer loyalties of 70% and 60%. If, when they open (at the same time), 80% of all customers go to Burger King, how many of the customers will go to O'Donalds after two trips?
So about 2/3 of the customers are going to O-Dees after two trips.
This repetition of matrices to find data is called a Markov Chain. Markov Chains are statistic models whose event probabilities are based on the previous event.
The matrix [(0.75, 0.25) (0.75, 0.25)] from the first problem is called a steady-state matrix, because it is the convergence of the transition matrix and cannot be altered further by the transition matrix.
Transition matrices and network matrices are used in a LOT of things: communication, business, competitions, ecology, psychology, transportation, and even biology.
~~~~~~~~
Crazy, right? I hope you like this as much as I do.
Stay coolio
John
Wednesday, April 9
Infinite Series (and Sequences) (cont.) (see first post) (parentheses)
When nobody knew anything about my blog except for my friend and some German Menschen (some of my first internet traffic came via Germany, strangely enough), I had a post about infinite serieses*. I found something interesting that my math teacher recommended I put in here, and as that topic was infinite sequences, I decided to put it in here.
Here is one of the problems:
Let's make a house of cards!
Write a formula for the sequence representing the number of cards at each stage.
First method is to make a chart.
Stage- 1 2 3 4...
Cards- 2 7 15 26...
+5 +8 +11
Each stage increases by 3 more than the last increase. Now I'm sure there's an algebraic way to solve it from there, but my method is much more interesting.
Look at the direction that the cards face-- I marked them with lines. What's the sequence that the directions make?
Stage- 1 2 3 4
Dir 1- 1 3 6 10
Dir 2- 1 3 6 10
Dir 3- 0 1 3 6
We know those sequences! Those are triangular numbers, denoted by (y=n(n+1)/2). Because one is offset to the left, we modify the formula a bit to (y=n(n-1)/2). By definition, we can add these three formulas together to get:
y=n(3n+1)/2
Another thing we thought about in class were divergent sequences with really weird sums. For example, 1+2+3+4... is equal to -1/12, while 1+2+4+8... is equal to -1. Here's why:
For the first, imagine three sequences:
S1=1-1+1-1+1-1+1...
S2=1-2+3-4+5-6...
S=1+2+3+4+5...
Unfortunately, S1 orbits on the period of 1 and 0. So we have to use other methods. Watch this:
S1 + S1 = 1 - 1 + 1 - 1 + 1 - 1 ....
+ 1 - 1 + 1 - 1 + 1
= 1 + 0 + 0 + 0 + 0 + 0... = 1
So two times S1 is one, so S1 is 0.5.
And then, there's S2.
S2 + S2 = 1 - 2 + 3 - 4 + 5 - 6 + 7 ...
+ 1 - 2 + 3 - 4 + 5 - 6 ...
= 1 - 1 + 1 - 1 + 1 - 1 ...
Thereby establishing that S2 is 0.25.
Then watch this!
S - S2 = 1 + 2 + 3 + 4 + 5 + 6 + 7 ...
-1 + 2 - 3 + 4 - 5 + 6 - 7
= 4 + 8 + 12 + 16 + 20 + 24 + 28 ...
which is 4 times S. We end with:
S - 0.25 = 4S
S = -1/12
Wow! Amazing! Literally impossible!
There's probably some reason that it's not true, but who cares? It's just time to marvel at the effects of calculus on algebra!
The next one on the list (that my friend learned from a high school teacher) is
S = 1 + 2 + 4 + 8 + 16 + 32 + 64
And so we use the same method, in theory.
S - S = 1 + 2 + 4 + 8 + 16 + 32 + 64 ...
- 1 - 2 - 4 - 8 - 16 - 32..
= 1 + 1 + 2 + 4 + 8 + 16 + 32...
And so
S - S = S + 1
S = -1
Another impossible sum! If any people disagree they will be ridiculed forever! I'm kidding- just give me a reason that I understand.
Stay coolio,
John
PS.: This post took FOREVER
Here is one of the problems:
Let's make a house of cards!
First method is to make a chart.
Stage- 1 2 3 4...
Cards- 2 7 15 26...
+5 +8 +11
Each stage increases by 3 more than the last increase. Now I'm sure there's an algebraic way to solve it from there, but my method is much more interesting.
Look at the direction that the cards face-- I marked them with lines. What's the sequence that the directions make?
Stage- 1 2 3 4
Dir 1- 1 3 6 10
Dir 2- 1 3 6 10
Dir 3- 0 1 3 6
We know those sequences! Those are triangular numbers, denoted by (y=n(n+1)/2). Because one is offset to the left, we modify the formula a bit to (y=n(n-1)/2). By definition, we can add these three formulas together to get:
y=n(3n+1)/2
Another thing we thought about in class were divergent sequences with really weird sums. For example, 1+2+3+4... is equal to -1/12, while 1+2+4+8... is equal to -1. Here's why:
For the first, imagine three sequences:
S1=1-1+1-1+1-1+1...
S2=1-2+3-4+5-6...
S=1+2+3+4+5...
Unfortunately, S1 orbits on the period of 1 and 0. So we have to use other methods. Watch this:
S1 + S1 = 1 - 1 + 1 - 1 + 1 - 1 ....
+ 1 - 1 + 1 - 1 + 1
= 1 + 0 + 0 + 0 + 0 + 0... = 1
So two times S1 is one, so S1 is 0.5.
And then, there's S2.
S2 + S2 = 1 - 2 + 3 - 4 + 5 - 6 + 7 ...
+ 1 - 2 + 3 - 4 + 5 - 6 ...
= 1 - 1 + 1 - 1 + 1 - 1 ...
Thereby establishing that S2 is 0.25.
Then watch this!
S - S2 = 1 + 2 + 3 + 4 + 5 + 6 + 7 ...
-1 + 2 - 3 + 4 - 5 + 6 - 7
= 4 + 8 + 12 + 16 + 20 + 24 + 28 ...
which is 4 times S. We end with:
S - 0.25 = 4S
S = -1/12
Wow! Amazing! Literally impossible!
There's probably some reason that it's not true, but who cares? It's just time to marvel at the effects of calculus on algebra!
The next one on the list (that my friend learned from a high school teacher) is
S = 1 + 2 + 4 + 8 + 16 + 32 + 64
And so we use the same method, in theory.
S - S = 1 + 2 + 4 + 8 + 16 + 32 + 64 ...
- 1 - 2 - 4 - 8 - 16 - 32..
= 1 + 1 + 2 + 4 + 8 + 16 + 32...
And so
S - S = S + 1
S = -1
Another impossible sum! If any people disagree they will be ridiculed forever! I'm kidding- just give me a reason that I understand.
Stay coolio,
John
PS.: This post took FOREVER
Friday, April 4
GAME THEORY
I was looking through a Barnes and Noble science section for a book on quantum theory (DON'T JUDGE), and I found a book entitled "Game Theory". I began to look through it and found it to be very interesting. Although I didn't find a good (and easy to understand) book on QT, I almost got the Game Theory.
In game theory, only two things define a game-
-there are two or more players...
-who interact to maximize a 'Utility'.
In games, Utility are the 'points'-- or, if no points, a numerical representation of the situation they're in. Usually it's an estimate.
Let's give an example.
There are two prisoners A and B. Together, they committed a crime for which they could get 10 years in prison. However, they are each offered a deal in which they can confess and testify against their partner (defect) or refuse to admit it (refuses). This is the deal to both of them:
a) If you defect and your friend refuses, you escape free and your friend gets 20 years.
b) If you both defect, you both get 5 years.
c) If you both refuse, you get 10 years.
Let's analyze!
If your friend will defect, your best option is to defect too, because it reduces your sentence by 15 years. However, if your friend will likely refuse, you should defect, as it will reduce your sentence by 10 years. Your best option is to defect, because the average between your possible sentences will reduce by 7.5 years than if you refuse. Think of it this way-
We could also plot it on a tree.
An interesting property of the PD is that the players technically do not interact-- it's what they do when they don't interact that makes it an interesting game.
There's a concept called Nash Equilibrium that's relatively important to game theory. From what I can tell, it's a situation where no players want to change their strategy. In a way, it means that they won't gain anything by changing their strategy.
A NE in Prisoner's Dilemma is, let's say, both players choose to defect. If either player decides to change their strategy, they'll lose.
There's also another game called Morra that you may have played. This is an interesting game that is played like rock-paper-scissors.
In Morra, only two players compete. So, on the count of whatever, each player holds up a number on their fingers from one to ten. If the sum of their numbers is even, one player wins; and vice versa.
Here's a chart I created-
In game theory, only two things define a game-
-there are two or more players...
-who interact to maximize a 'Utility'.
In games, Utility are the 'points'-- or, if no points, a numerical representation of the situation they're in. Usually it's an estimate.
Let's give an example.
There are two prisoners A and B. Together, they committed a crime for which they could get 10 years in prison. However, they are each offered a deal in which they can confess and testify against their partner (defect) or refuse to admit it (refuses). This is the deal to both of them:
a) If you defect and your friend refuses, you escape free and your friend gets 20 years.
b) If you both defect, you both get 5 years.
c) If you both refuse, you get 10 years.
Let's analyze!
If your friend will defect, your best option is to defect too, because it reduces your sentence by 15 years. However, if your friend will likely refuse, you should defect, as it will reduce your sentence by 10 years. Your best option is to defect, because the average between your possible sentences will reduce by 7.5 years than if you refuse. Think of it this way-
This is called a matrix, if you don't know. But I'm assuming that you do.
An interesting property of the PD is that the players technically do not interact-- it's what they do when they don't interact that makes it an interesting game.
There's a concept called Nash Equilibrium that's relatively important to game theory. From what I can tell, it's a situation where no players want to change their strategy. In a way, it means that they won't gain anything by changing their strategy.
A NE in Prisoner's Dilemma is, let's say, both players choose to defect. If either player decides to change their strategy, they'll lose.
There's also another game called Morra that you may have played. This is an interesting game that is played like rock-paper-scissors.
In Morra, only two players compete. So, on the count of whatever, each player holds up a number on their fingers from one to ten. If the sum of their numbers is even, one player wins; and vice versa.
Here's a chart I created-
Notice that the number they pick doesn't matter-– only if it's even or odd does.The odd player should do the opposite of the even player, but the even player should do the same as the odd. There is no real 'better strategy', unless you somehow read your opponent's mind, or predict the future.
Anyway, I guess that's it! There are tons of other good games-- Rock Paper Scissors, Nim, 2/3 the Average, and Fair Division (Cake Cutting). You acan look at them if you want.
Stay coolio, John
*PS: Sorry if this was a bad post-- Game Theory is extremely general*
Friday, March 28
Orbits!
OK, this is a really interesting post for me. Just stick with it, OK?
In math, there are two types of orbits:
1) An elliptical path traced by an object due to gravitational pull towards another object. AKA the orbit that you know.
2) A repetition of a function infinitely upon itself. (this term might be outdated- I found the lesson in a precalculus book at my college-aged cousins' house)
For orbit #1, an orbit is elliptical due to two factors:
1) Gravity is imperfect.
2) the way that an object enters (or forms in) the gravitational area.
Anyway, the point is that the object that it orbits around is a focus of that ellipse. The foci are the two points that determine the ellipse-- the sum of the distances from any point on the ellipse to each of the foci is constant.
In math, there are two types of orbits:
1) An elliptical path traced by an object due to gravitational pull towards another object. AKA the orbit that you know.
2) A repetition of a function infinitely upon itself. (this term might be outdated- I found the lesson in a precalculus book at my college-aged cousins' house)
For orbit #1, an orbit is elliptical due to two factors:
1) Gravity is imperfect.
2) the way that an object enters (or forms in) the gravitational area.
Anyway, the point is that the object that it orbits around is a focus of that ellipse. The foci are the two points that determine the ellipse-- the sum of the distances from any point on the ellipse to each of the foci is constant.
If you think about it, the Sun isn't at the center of the solar system–– it's at one of the foci.
Here's a good problem about it.
Denying the laws of probability and physics itself, let's say the planets in our solar system are perfectly lined up to one side of the sun. The center of the ellipse is approximately 1.5 million km from the center of the sun. If Earth is at its closest point to the sun (148 million km), and the center of gravity of the solar system remains where it is no matter where the planets travel (which is a lie), what is the furthest point of Earth's orbit from the sun?
In the ellipse above, A and B are the foci, D is the center, and C and E are points on the major and minor axes respectively.
Anyhow, in this case, AD is equal to 1.5 million kilometers and EA is equal to 148 million kilometers. The sun is at A and Earth is at E.
Since the furthest point is basically the point on the other side of point B, the formula for the farthest point would be:
( (EA) + (AD) ) * 2 - (EA)
Which is about 151 million km, or an accurate-ish 93.8 million miles.
Another thing you might want to know about ellipses is that in the above example (pretend the scale is off), ED=AC=(AD)^2 + (CD)^2.
~~~~
Soooo, now to the other orbit.
Function orbits are similar to orbits: they go around and around a particular value. Now, to explain them.
Imagine a function f(x) for any value x1. Now imagine f(f(x1)). Then f(f(f(x1))). Continue this pattern until you are 106 years old. The orbit of f(x) for that value of x1 would be the infinite sequence
x, f(x), f(f(x)).... on until you are 106. Or really, infinity years old. The last (or technically last) term of that sequence would be called the limit of the orbit, because the sequence would get infinitely close to the limit but not to the limit.
The limits are also called 'fixed points', because if x1 is equal to its limit, it goes automatically to the limit. Therefore, the limit becomes 'fixed', as its position never changes after the first term.
If you think about it, the fixed points are all on the line y=x, as shown for f(x)= sqrt(x):
In fact, this is a good function to show you something about.
For f(x)=sqrt(x):
For the x1 values of 0<x1<1, what is the limit?
For the x1 values of x>1, what is the limit?
As you can see, both limits to the domain containing non-fixed points are 1. So, 1 is an attracting limit while 0 is repelling.
There are a couple important uses of orbits.
What is the value of 1+(2/(1+(2/(1+(2/...
This is the limit of the orbit 1+(2/x). Calculating the value of the limit would be:
1+(2/x) = x
x^2 - x - 2 = 0
x= 2, -1
Since all of the signs are positive, the root must be positive 2.
*Note*- The above problem could be thought of as the limit of (2/(1+x)) plus one.
The easier way to explain population is through orbits. Population prediction is really important for people in government, and they use dynamic systems to answer their questions. Here's an example of a model:
f(x+1)= 4 * f(x) * (1 - f(x))
where f(x) is a decimal less than one representing the current population. This function is true because of four things:
1)–– (1-f(x)) is a representation of death, especially by starvation or sickness. This would be true because as population goes up, resources get used quicker and lead to a severe lack of supplies.
2)–– f(x) is a representation of birth, which also increases as the population increases.
3)–– 4 is needed to multiply because 0.5 is lost twice when the other terms are multiplied.
4)–– The function is recursive because we're trying to find the population next year, not any general year.
~~~~~
Have fun pondering over what I'm trying to explain!
Stay coolio,
John
Wednesday, March 26
Your Least Favorite Post
That's right... we're doing
So here are some tips for using the ID's--
1) Memorize those formulae- esp. sum and difference identities.
2) Simplify to sines and cosines-- using algebra and reciprocal ID's. This is probably the most important step.
3) Use algebra to simplify to the least possible amount of terms.
4) Use a calculator or something to do the rest. (if solving for variable)
Usually, the point of the identities is to
a) prove an identity/theorem or
b) solve for a variable.
Like above, you have to use all of the identities, mostly reciprocals.
Although it's one of the most annoying parts of math, it's definitely worth knowing.
Another way to solve it is graphing, but that takes away all the coolness of it. Basically, you can find if the graphs of (cot(x)+tan(x)) and (sec(x)csc(x)) are the same.
I might do something with functions and orbits later. Sorry for not posting in a while.
Stay coolio, John
Thursday, March 20
Late Pi Day
Pie? Like the food?
OK, you've probably heard that before, as Pi Day is now more conspicuous in terms of holidays. Happy 6-days-too-late-for-Pi Day!
The approximate ratios for pi are:
3 digits: 22/7
4 digits: 245/78
5 digits: 333/106
6 and 7 digits: 355/113
continued...
38 digits: 2,646,693,125,139,304,345 / 842,468,587,426,513,207
Well, quintillions are pretty accurate, right?
At digit 763, there are 6 nines in a row. This is the Feynman point.
To find the circumference of a circle the size of the universe to within the radius of a single proton, you only need 39 digits. Although that seems like a lot, it really isn't.
Chao Lu from China memorized 67900 digits of pi. Nice use of time, Chao! Especially considering the last fact!
A ten year old actually memorized 410 digits of pi. Either he felt the urge to learn all of them or his parents are gigantic perfectionists.
Pi is equal to...
6 * sqrt(sum (1-inf) (1/n^2) )
4 * (sum (1-inf) ((-1)^n /(2n+1)))
Although pi is determined by a ratio, it cannot be expressed using a ratio. Therefore, the circumference and/or the diameter must be irrational in a circle.
In the first six million digits of pi, five is the most common and zero is the least common. In the first million, five is the most common and seven is the least common.
Pi is technically mentioned in the bible- see 1 Kings 7:23.
Pi has been referenced in a huge amount of books, TV shows, and movies.
Extremely Cool Sites:
The Pi-search page- This finds certain strings of digits from the first 200 million digits of pi. Extremely cool website.
More Links
Keep calm and guess again!
OK, you've probably heard that before, as Pi Day is now more conspicuous in terms of holidays. Happy 6-days-too-late-for-Pi Day!
The approximate ratios for pi are:
3 digits: 22/7
4 digits: 245/78
5 digits: 333/106
6 and 7 digits: 355/113
continued...
38 digits: 2,646,693,125,139,304,345 / 842,468,587,426,513,207
Well, quintillions are pretty accurate, right?
At digit 763, there are 6 nines in a row. This is the Feynman point.
To find the circumference of a circle the size of the universe to within the radius of a single proton, you only need 39 digits. Although that seems like a lot, it really isn't.
Chao Lu from China memorized 67900 digits of pi. Nice use of time, Chao! Especially considering the last fact!
A ten year old actually memorized 410 digits of pi. Either he felt the urge to learn all of them or his parents are gigantic perfectionists.
Pi is equal to...
6 * sqrt(sum (1-inf) (1/n^2) )
4 * (sum (1-inf) ((-1)^n /(2n+1)))
Although pi is determined by a ratio, it cannot be expressed using a ratio. Therefore, the circumference and/or the diameter must be irrational in a circle.
In the first six million digits of pi, five is the most common and zero is the least common. In the first million, five is the most common and seven is the least common.
Pi is technically mentioned in the bible- see 1 Kings 7:23.
Pi has been referenced in a huge amount of books, TV shows, and movies.
Extremely Cool Sites:
The Pi-search page- This finds certain strings of digits from the first 200 million digits of pi. Extremely cool website.
More Links
Keep calm and guess again!
Friday, March 7
Problems of the Week 2 Answers
1. The answer to this is really obvious. The sum of n (1/n)'s is 1, so you need k=1000 ones to get 1000.
2. By definition, all multiples of x can be represented as Nx mod x, where N is an integer. Working backward, we find out that the code must be a multiple of 7, 8, and 9. The only three digit number with this property is 7*8*9= 504.
3. Let's replace the cost of a cone with x. Al must have (x-24) cents and Bob must have (x-2) cents. If Bob is only two cents short and the sum of their money is less than x, then Al must have 0 cents or 1 cent. Because Al took at least some money from his bank, he took out one cent; solving for x, we find that the cost is 25 cents.
4. This problem is simple replacement. We can take out the one to get 22 as a solution; and, if you take out 2, 3, and 4 and replace them with 24, you get 20. You can't add 25 because only one five follows, so those are your only solutions.
5. Two digit numbers with digits (xy) are written as 10x+y. Therefore the equation for their ages are:
10x+y+(41-14)=10y+x. One of the solutions is already (1, 4), and when we simplify we get
y=x+3. The next positive integer solution would be (2, 5),and therefore the answer is 11 years later.
6. When you graph 0<y<2, 0<x<2, and abs(y-x)<1, you get:
The green area takes up 3/4 of the 2x2 square, so the probability is 3 in 4.
7. After the first repetition, there are three digits. So after two repetitions, there are exactly four possibilities for the number: 033, 123, 213, and 303. However, 033 and 213 are null because no number simplifies to either of the two. 123 and 303 both go to 123 again.
8. For the sake of understanding what I'm saying, let's use the @ symbol in place of 'plus or minus'. abs(x) in this case simplifies to @x, abs(1@x) simplifies to @1@x, and abs(2@1@x) simplifies to @2@1@x=1. The solutions to this are @4, @2, and @0.
9. Drawing out the hexagon, it looks like this:
Notice that the corners are equilateral triangles of side lengths 9, 14, and 10. If you think about it, the other equilateral triangle will have corner triangles of 7, 11, and 6. The side length of the large triangle will consist of the side lengths of two smaller triangles and the side inbetween them. That would make the triangle's side length equal 7+14+6=6+10+11=11+9+7= 27 units.
10. Draw this out too.
 Because FA is tangent to circle C at point F, radius FC is perpendicular to FA. This forms right triangle CAF, with hypotenuse CA and legs FA and FC. We know that FC is 3 units, and AC is 5 units, so therefore FA is 4 units long.
Because FA is tangent to circle C at point F, radius FC is perpendicular to FA. This forms right triangle CAF, with hypotenuse CA and legs FA and FC. We know that FC is 3 units, and AC is 5 units, so therefore FA is 4 units long.
Sorry for the kind-of bad explanations I made. I tried, at least!
Stay coolio,
John
PS: Credit to SketchBookExpress and GeoGebra for the illustrations.
2. By definition, all multiples of x can be represented as Nx mod x, where N is an integer. Working backward, we find out that the code must be a multiple of 7, 8, and 9. The only three digit number with this property is 7*8*9= 504.
3. Let's replace the cost of a cone with x. Al must have (x-24) cents and Bob must have (x-2) cents. If Bob is only two cents short and the sum of their money is less than x, then Al must have 0 cents or 1 cent. Because Al took at least some money from his bank, he took out one cent; solving for x, we find that the cost is 25 cents.
4. This problem is simple replacement. We can take out the one to get 22 as a solution; and, if you take out 2, 3, and 4 and replace them with 24, you get 20. You can't add 25 because only one five follows, so those are your only solutions.
5. Two digit numbers with digits (xy) are written as 10x+y. Therefore the equation for their ages are:
10x+y+(41-14)=10y+x. One of the solutions is already (1, 4), and when we simplify we get
y=x+3. The next positive integer solution would be (2, 5),and therefore the answer is 11 years later.
6. When you graph 0<y<2, 0<x<2, and abs(y-x)<1, you get:
The green area takes up 3/4 of the 2x2 square, so the probability is 3 in 4.
7. After the first repetition, there are three digits. So after two repetitions, there are exactly four possibilities for the number: 033, 123, 213, and 303. However, 033 and 213 are null because no number simplifies to either of the two. 123 and 303 both go to 123 again.
8. For the sake of understanding what I'm saying, let's use the @ symbol in place of 'plus or minus'. abs(x) in this case simplifies to @x, abs(1@x) simplifies to @1@x, and abs(2@1@x) simplifies to @2@1@x=1. The solutions to this are @4, @2, and @0.
9. Drawing out the hexagon, it looks like this:
10. Draw this out too.

Sorry for the kind-of bad explanations I made. I tried, at least!
Stay coolio,
John
PS: Credit to SketchBookExpress and GeoGebra for the illustrations.
Thursday, March 6
Problems of the Week (or General Period of Time) 2
Here're some problems from the Math Contests book I got for winning a contest–– see if you can do them!
1. (Easy) In the ordered sequence of positive integers, {1, 2, 2, 3, 3, 3, 4, 4, 4, 4....}, each positive integer n occurs in a block of n terms. For what value of k is the sum of the reciprocals of the first k terms equal to 1000?
2. (Easy) My area code is a positive three-digit number. Add 7 to it and the result is divisible by y. Add 8 to it and the result is divisible by 8. Add 9 to it and the result is divisible by 9. What is my area code?
3. (Easy-Moderate) Al and Bob each took some money from their piggy bank to get ice cream. Al was 24 cents short of a cone and Bob was 2 cents short. They pooled their money just to find out that they were still short. How much money did Bob take out of his bank? (sorry the names are boring, the original ones were Rufus and Dufus. I thought those would be stupid enough to take away the point of the problem...)
4. (Easy-Moderate) The factorial 23! can be written as the product of n consecutive integers such that 1< n <23. What are the possible values of n?
5. (Easy-Moderate) On his birthday, Brian was fourteen and his father was 41. What's the next time their ages will be the 'reverse' of each other? (Don't trial and error!)
6. (Moderate-Hard) Both x and y are positive numbers less than 2. Every positive number less than 2 is equally likely to be x and ditto y. What is the probability that x and y differ by less than one?
7. (Moderate) Form any positive integer n with less than 10 digits. Form the three digit number x where the hundreds digit is equal to the number of even digits in that number, the tens is equal to the number of odd digits, and the ones digit is equal to the sum of the other two. Then replace the original number with the new one. If this process is repeated infinitely, what number remains?
8. (Moderate-Hard) What are the real values of x that satisfy abs(2 - abs(1- abs(x))) = 1?
9. (Hard) An equiangular hexagon with side-lengths 9, 11, 10, 6, 14, and 7 (going clockwise) can be inscribed in an equilateral triangle with side-length 30. What is the side length of the other possible triangles?
10. (Hard) Two externally tangent circles have radii 2 and 3 units. If there is a segment whose endpoints are the center of the small circle and the point at which it is tangent to the larger circle, what is the segment's length?
The answers will be posted tomorrow evening!
Stay coolio,
John
1. (Easy) In the ordered sequence of positive integers, {1, 2, 2, 3, 3, 3, 4, 4, 4, 4....}, each positive integer n occurs in a block of n terms. For what value of k is the sum of the reciprocals of the first k terms equal to 1000?
2. (Easy) My area code is a positive three-digit number. Add 7 to it and the result is divisible by y. Add 8 to it and the result is divisible by 8. Add 9 to it and the result is divisible by 9. What is my area code?
3. (Easy-Moderate) Al and Bob each took some money from their piggy bank to get ice cream. Al was 24 cents short of a cone and Bob was 2 cents short. They pooled their money just to find out that they were still short. How much money did Bob take out of his bank? (sorry the names are boring, the original ones were Rufus and Dufus. I thought those would be stupid enough to take away the point of the problem...)
4. (Easy-Moderate) The factorial 23! can be written as the product of n consecutive integers such that 1< n <23. What are the possible values of n?
5. (Easy-Moderate) On his birthday, Brian was fourteen and his father was 41. What's the next time their ages will be the 'reverse' of each other? (Don't trial and error!)
6. (Moderate-Hard) Both x and y are positive numbers less than 2. Every positive number less than 2 is equally likely to be x and ditto y. What is the probability that x and y differ by less than one?
7. (Moderate) Form any positive integer n with less than 10 digits. Form the three digit number x where the hundreds digit is equal to the number of even digits in that number, the tens is equal to the number of odd digits, and the ones digit is equal to the sum of the other two. Then replace the original number with the new one. If this process is repeated infinitely, what number remains?
8. (Moderate-Hard) What are the real values of x that satisfy abs(2 - abs(1- abs(x))) = 1?
9. (Hard) An equiangular hexagon with side-lengths 9, 11, 10, 6, 14, and 7 (going clockwise) can be inscribed in an equilateral triangle with side-length 30. What is the side length of the other possible triangles?
10. (Hard) Two externally tangent circles have radii 2 and 3 units. If there is a segment whose endpoints are the center of the small circle and the point at which it is tangent to the larger circle, what is the segment's length?
The answers will be posted tomorrow evening!
Stay coolio,
John
Wednesday, March 5
Analysis of Solving Mazes (logic edition)
How do you solve a simple maze without knowing what the maze looks like from above?
Well, let's first define the maze. Let's say the maze (I'll call it the Johnesian maze) is a rectangular 'grid' with 2 openings on edges of the grid (for start and exit), and enough walls taken out as to provide at least one path between the openings. Remember that these features define the maze–– the grid is a Johnesian maze only if it has exactly two openings on the edge, and enough grid-walls are removed to provide a path to each.
To show you the first and easiest method, let's think about the lines (note: lines are connected strips walls, not the walls themselves) in the maze. There must be two lines, because the two lines end at the start and finish and cannot be connected in the middle (or else there is no solution path). There can also be island lines, or lines that touch neither the start nor finish.
By that logic, there are two lines that touch both the start and the finish. Therefore, you can just follow one of the walls beside the start until you eventually reach the finish. This is called the left (or right)-hand rule.
For the second, the answer is much less confusing. If one can tell the difference between the start and the finish, and discern therefore that the start is not the finish, you can just pick completely random paths and eventually (after infinity) it is guaranteed that the finish is found. Of course that solution assumes that there is unlimited food and water. This solution is the Random Mouse.
The third is more difficult. As you walk down a passage, draw a line behind you to mark your path. When you hit a dead end turn around and go back the way you came. When you encounter a junction you haven't visited before, pick a new passage at random. If you're walking down a new passage and encounter a junction you have visited before, treat it like a dead end and go back the way you came so that you won't go around in circles or missing passages. If walking down a passage you have visited before (i.e. marked once) and you encounter a junction, take any new passage if one is available, otherwise take an "old" one. Every passage will be either empty (if not visited yet), marked once, or marked twice (if you were forced to backtrack). When you reach the solution, the paths which were marked exactly once will indicate the direct way back to the start. If the maze has no solution, you'll find yourself back at the start with all passages marked twice. It's kind of complicated, but I'm sure it works. BTW, this is called the Tremaux algorithm.
If you can look from above, a good strategy is to fill out all dead ends or nooses (eg, places where you must backtrack to find a solution). Then you fill in the places that lead only to dead ends and nooses. And etc, until the only paths not filled in are solutions.
The last one is the Pledge Algorithm. The idea is to try to always go in one chosen direction, if you do not turn more than 359 degrees in any direction.
So let's measure our angles- a left turn is worth -1 and a right turn is worth 1, and you add each on to your 'turn count' whenever you turn. Choose a direction that goes towards the finish, and calibrate it to turn count=0, -4, 4, and so on. Just know that no multiple of 4 that is not 0 is equal to 0, just for this algorithm. In the algorithm:
1) If turn count = 0 and path ahead is open, then go forward.
2) If turn count is 0 and there is a wall directly ahead, then follow that wall in a random direction until turn count=0.
This algorithm is confusing and difficult, but it works.
NOTE: Only one of these methods is mine, and a ton of them I don't understand at all. If I have left something out, sorry!
Good sites:
Labyrinth.htm
Wikipedia- Maze solving algorithms
I bet your brain exploded a while ago, so I might as well just shut up now. See ya!
Stay coolio,
John
Well, let's first define the maze. Let's say the maze (I'll call it the Johnesian maze) is a rectangular 'grid' with 2 openings on edges of the grid (for start and exit), and enough walls taken out as to provide at least one path between the openings. Remember that these features define the maze–– the grid is a Johnesian maze only if it has exactly two openings on the edge, and enough grid-walls are removed to provide a path to each.
To show you the first and easiest method, let's think about the lines (note: lines are connected strips walls, not the walls themselves) in the maze. There must be two lines, because the two lines end at the start and finish and cannot be connected in the middle (or else there is no solution path). There can also be island lines, or lines that touch neither the start nor finish.
By that logic, there are two lines that touch both the start and the finish. Therefore, you can just follow one of the walls beside the start until you eventually reach the finish. This is called the left (or right)-hand rule.
For the second, the answer is much less confusing. If one can tell the difference between the start and the finish, and discern therefore that the start is not the finish, you can just pick completely random paths and eventually (after infinity) it is guaranteed that the finish is found. Of course that solution assumes that there is unlimited food and water. This solution is the Random Mouse.
The third is more difficult. As you walk down a passage, draw a line behind you to mark your path. When you hit a dead end turn around and go back the way you came. When you encounter a junction you haven't visited before, pick a new passage at random. If you're walking down a new passage and encounter a junction you have visited before, treat it like a dead end and go back the way you came so that you won't go around in circles or missing passages. If walking down a passage you have visited before (i.e. marked once) and you encounter a junction, take any new passage if one is available, otherwise take an "old" one. Every passage will be either empty (if not visited yet), marked once, or marked twice (if you were forced to backtrack). When you reach the solution, the paths which were marked exactly once will indicate the direct way back to the start. If the maze has no solution, you'll find yourself back at the start with all passages marked twice. It's kind of complicated, but I'm sure it works. BTW, this is called the Tremaux algorithm.
If you can look from above, a good strategy is to fill out all dead ends or nooses (eg, places where you must backtrack to find a solution). Then you fill in the places that lead only to dead ends and nooses. And etc, until the only paths not filled in are solutions.
The last one is the Pledge Algorithm. The idea is to try to always go in one chosen direction, if you do not turn more than 359 degrees in any direction.
So let's measure our angles- a left turn is worth -1 and a right turn is worth 1, and you add each on to your 'turn count' whenever you turn. Choose a direction that goes towards the finish, and calibrate it to turn count=0, -4, 4, and so on. Just know that no multiple of 4 that is not 0 is equal to 0, just for this algorithm. In the algorithm:
1) If turn count = 0 and path ahead is open, then go forward.
2) If turn count is 0 and there is a wall directly ahead, then follow that wall in a random direction until turn count=0.
This algorithm is confusing and difficult, but it works.
NOTE: Only one of these methods is mine, and a ton of them I don't understand at all. If I have left something out, sorry!
Good sites:
Labyrinth.htm
Wikipedia- Maze solving algorithms
I bet your brain exploded a while ago, so I might as well just shut up now. See ya!
Stay coolio,
John
Monday, March 3
Squares!
Well, by squares, I obviously mean square numbers, right?
Welcome back to your favorite site! I'm going to do a rather short post today, as I can't really think of much to do.
Here's something I found out a couple of days ago.
For any integer, then x^2 is either a multiple of 4 or one more than a multiple of 4.
Proof: This theory depends on whether that integer is odd or even. Let's represent the set of any integer as N.
odd– (2N+1)^2=4(N^2)+4(N)+1=4(N^2+N)+1=4(N)+1
even– (2N)^2=4(N^2)=4(N)
As one can see, an odd integer squared is one more than four times another integer, and an even integer squared is four times another integer. Isn't that weird?
Another odd thing is that the sums of the first few cubes is always the square of the sum of their base numbers. For example,
1^3 + 2^3 = (1+2)^2
1^3 + 2^3 + 3^3 = (1+2+3)^2
1^3 + 2^3 + 3^3 + 4^3 = (1+2+3+4)^2
Speaking of shape--ish numbers, every square is the sum of two consecutive triangles. I wonder if the sum of two consecutive squares is a pentagonal? Or if you can figure out hyper-cubic numbers? Probably you can-- I'll update that later.
The difference between perfect squares is always odd. (n+1)^2 - n^2 = 2n+1, so if n is an integer, the difference is odd (and the squares are perfect squares).
There's a weird pattern in the squares of all of the integers from 969 to 1000. What is it? (Look closely; no, it's not the thousands digits)
An easy way to approximate a square root without a calculator is by:
1) guessing the root
2) dividing your guess into the original
3) finding the mean of the result and the guess
4) and repeating steps 2 to 4 with what you get.
All square numbers end with the digits 1, 4, 6, 9, 25, or 00.
Stay coolio,
John
PS: If you have a Google account, please follow me through the button on the right! Enter your email into the box to get notifications about new posts! Preferably both please!
Welcome back to your favorite site! I'm going to do a rather short post today, as I can't really think of much to do.
Here's something I found out a couple of days ago.
For any integer, then x^2 is either a multiple of 4 or one more than a multiple of 4.
Proof: This theory depends on whether that integer is odd or even. Let's represent the set of any integer as N.
odd– (2N+1)^2=4(N^2)+4(N)+1=4(N^2+N)+1=4(N)+1
even– (2N)^2=4(N^2)=4(N)
As one can see, an odd integer squared is one more than four times another integer, and an even integer squared is four times another integer. Isn't that weird?
Another odd thing is that the sums of the first few cubes is always the square of the sum of their base numbers. For example,
1^3 + 2^3 = (1+2)^2
1^3 + 2^3 + 3^3 = (1+2+3)^2
1^3 + 2^3 + 3^3 + 4^3 = (1+2+3+4)^2
Speaking of shape--ish numbers, every square is the sum of two consecutive triangles. I wonder if the sum of two consecutive squares is a pentagonal? Or if you can figure out hyper-cubic numbers? Probably you can-- I'll update that later.
The difference between perfect squares is always odd. (n+1)^2 - n^2 = 2n+1, so if n is an integer, the difference is odd (and the squares are perfect squares).
There's a weird pattern in the squares of all of the integers from 969 to 1000. What is it? (Look closely; no, it's not the thousands digits)
An easy way to approximate a square root without a calculator is by:
1) guessing the root
2) dividing your guess into the original
3) finding the mean of the result and the guess
4) and repeating steps 2 to 4 with what you get.
All square numbers end with the digits 1, 4, 6, 9, 25, or 00.
Stay coolio,
John
PS: If you have a Google account, please follow me through the button on the right! Enter your email into the box to get notifications about new posts! Preferably both please!
Tuesday, February 25
Yes I'm Still Alive!
HEY!
Sorry I couldn't get back sooner... I tried to put up a post a couple times but it wouldn't save or publish the post. Anyhow, I'm back! I'll try to do a summary of last ones this time for yall.
Pigeonhole Principle-- the idea of putting pigeons in holes. If there are m pigeons in m holes, then––
a) either there is one pigeon per hole;
b) or there is an empty hole and a hole with more than one pigeon.
If there is m pigeons in n holes, and m>n, then there is at least one hole with more than one pigeon. If m<n, then there is at least one empty hole.
This is essentially the same thing as the socks from last week–– but the socks have magically transformed into birds (sheep or cotton plants would be much more fitting). You want at least two sheep in one of the holes-- so you make the number of sheep more than the number of holes.
Here's an interesting problem involving the pigeonhole principle that I found––
There are five points on the surface of a sphere. Prove that at least one hemisphere has four of the points in it.
In spherical geometry, any two points on the sphere determine a great circle that divides two hemispheres. According to the pigeonhole principle, at least two of the other points should be on one of the hemispheres. So, including the two on the great circle, there are four points on that hemisphere. Cool, right?
I also found a really cool logic/geometry problem in a book I read.
In a square swimming pool, there is a boy in the center. At one of the corners is a teacher that can run three times faster than the boy can swim. The boy can run faster than the teacher can. Logically, can the boy escape if the teacher must try to catch him? (Don't make assumptions!)
Because the boy is faster than the teacher on land, his goal is simply to reach the edge. If the boy tries to swim to the opposite corner, the teacher will arrive before he does. However, if he tries to swim to one of opposite edge midpoints, the teacher will arrive exactly as he does. If the teacher was a fraction slower, he would arrive before and escape. So, if he begins to travel towards one of the opposite midpoints, the teacher is forced to head there.
Consider the diagram.
If the boy swims n/3 units towards midpoint of BC, then the teacher is required to move to midpoint of AB because if they don't, the boy will escape that way. Then, the boy can swim n units towards CD and escape. Easy as pi.
Well, I guess that was a good long one for everybody. Again, sorry I haven't posted.
STay coolio,
John
Sorry I couldn't get back sooner... I tried to put up a post a couple times but it wouldn't save or publish the post. Anyhow, I'm back! I'll try to do a summary of last ones this time for yall.
Pigeonhole Principle-- the idea of putting pigeons in holes. If there are m pigeons in m holes, then––
a) either there is one pigeon per hole;
b) or there is an empty hole and a hole with more than one pigeon.
If there is m pigeons in n holes, and m>n, then there is at least one hole with more than one pigeon. If m<n, then there is at least one empty hole.
This is essentially the same thing as the socks from last week–– but the socks have magically transformed into birds (sheep or cotton plants would be much more fitting). You want at least two sheep in one of the holes-- so you make the number of sheep more than the number of holes.
Here's an interesting problem involving the pigeonhole principle that I found––
There are five points on the surface of a sphere. Prove that at least one hemisphere has four of the points in it.
In spherical geometry, any two points on the sphere determine a great circle that divides two hemispheres. According to the pigeonhole principle, at least two of the other points should be on one of the hemispheres. So, including the two on the great circle, there are four points on that hemisphere. Cool, right?
I also found a really cool logic/geometry problem in a book I read.
In a square swimming pool, there is a boy in the center. At one of the corners is a teacher that can run three times faster than the boy can swim. The boy can run faster than the teacher can. Logically, can the boy escape if the teacher must try to catch him? (Don't make assumptions!)
Because the boy is faster than the teacher on land, his goal is simply to reach the edge. If the boy tries to swim to the opposite corner, the teacher will arrive before he does. However, if he tries to swim to one of opposite edge midpoints, the teacher will arrive exactly as he does. If the teacher was a fraction slower, he would arrive before and escape. So, if he begins to travel towards one of the opposite midpoints, the teacher is forced to head there.
Consider the diagram.
If the boy swims n/3 units towards midpoint of BC, then the teacher is required to move to midpoint of AB because if they don't, the boy will escape that way. Then, the boy can swim n units towards CD and escape. Easy as pi.
Well, I guess that was a good long one for everybody. Again, sorry I haven't posted.
STay coolio,
John
Tuesday, February 11
Color Coding (both types)
When you hear the words 'color' and 'coding' together, you think of moms and control freaks, right? Well, in computer coding, there's actually a way of making every single color, sprinkled right in with set theory and hexadecimals.
When you want to express a color in coding, you use the amounts of Red, Blue, and Green. Therefore they call it the RGB Color System.
In coding, there are 255 different levels of each specified color. Since 256 is the square of 16, hexadecimal is the way to go in actually expressing the colors for the computer to register, convert, and show.
For the final input, you get a six digit number with some digits represented by letters from A through H. Basically, each color gets two digits to express its level. Examples:
#FF7000 is UVA ORANGE
#FF66FF is BREAST CANCER AWARENESS PINK
#00FF00 is MY FAVORITE COLOR (try to out what color this is! Don't cheat!)
Continuing a color streak, here's a problem about colors.
Let's say there are 8 red socks (#FF0000), 10 gray socks (#888888), 12 purple socks (#9933CC), and 14 white socks (#FFFFFF) in a drawer, all individually separated into a random pile. You just need a pair of socks–– any color, as long as they match color. However, either the lights or off or you're blind because you can't see what color each sock is. How many socks do you have to grab in order to make sure you get at least one match? How about 2?
Because you have to make absolutely sure, you think of the worst possible scenario, like all the color-coding control freaks at home. The worst possible scenario is that you'd get one of each sock. However, you need one pair, so you can add one and get 5 socks. As for two, you do the same thing: one from each of three colors and three of the last. Add one to get 7.
You want a pair of white socks, two pairs of gray socks, and a pair of red socks from that same drawer (and by the way, you put back the ones you took out). How many pairs do you have to pull out, at least?
This is basically the same idea: worst possible scenario and add one. Logically, you can get all of the purple socks without getting a correct pair at all. Since you want to have the most possible socks, you should get all of the white and gray socks too, and one red sock. That would give you 38 socks (by the way, you could also get all red, purple, and white socks and then 4 gray socks for the same answer).
Have a 'colorful' day in paradise...
Stay cool,
John
When you want to express a color in coding, you use the amounts of Red, Blue, and Green. Therefore they call it the RGB Color System.
In coding, there are 255 different levels of each specified color. Since 256 is the square of 16, hexadecimal is the way to go in actually expressing the colors for the computer to register, convert, and show.
For the final input, you get a six digit number with some digits represented by letters from A through H. Basically, each color gets two digits to express its level. Examples:
#FF7000 is UVA ORANGE
#FF66FF is BREAST CANCER AWARENESS PINK
#00FF00 is MY FAVORITE COLOR (try to out what color this is! Don't cheat!)
Continuing a color streak, here's a problem about colors.
Let's say there are 8 red socks (#FF0000), 10 gray socks (#888888), 12 purple socks (#9933CC), and 14 white socks (#FFFFFF) in a drawer, all individually separated into a random pile. You just need a pair of socks–– any color, as long as they match color. However, either the lights or off or you're blind because you can't see what color each sock is. How many socks do you have to grab in order to make sure you get at least one match? How about 2?
Because you have to make absolutely sure, you think of the worst possible scenario, like all the color-coding control freaks at home. The worst possible scenario is that you'd get one of each sock. However, you need one pair, so you can add one and get 5 socks. As for two, you do the same thing: one from each of three colors and three of the last. Add one to get 7.
You want a pair of white socks, two pairs of gray socks, and a pair of red socks from that same drawer (and by the way, you put back the ones you took out). How many pairs do you have to pull out, at least?
This is basically the same idea: worst possible scenario and add one. Logically, you can get all of the purple socks without getting a correct pair at all. Since you want to have the most possible socks, you should get all of the white and gray socks too, and one red sock. That would give you 38 socks (by the way, you could also get all red, purple, and white socks and then 4 gray socks for the same answer).
Have a 'colorful' day in paradise...
Stay cool,
John
Sunday, February 9
100 Pageviews!
Since my blog has hit 100 page views, I am going to do a binary special!
If you convert "John" into binary code and then back into base ten, you get '74 111 104 110', or '1,248,815,214' without letter spacing.
Some people actually get in trouble for copying distribution codes (in binary) and converting them into regular letters in order to redistribute them–– so technically, they're illegal!!!
2^x binary codes can be made x bits (binary digits) long, because there are two digit options per bit.
There are 3 main bases in the number system: binary (base 2), decimal (base 10), and hexadecimal (base 16). Hexadecimal is used to express binary numbers up to 4 bits long.
HEXADECIMAL DRUM SET–– http://www.mathsisfun.com/games/hex-drums.html
Math is Fun is a cool website to find stuff like this on
Sorry about subscribing issues, I'll try to fix that. Thanks to my sole follower, Ben K., for finding a way around that. See ya.
Stay coolio,
John
If you convert "John" into binary code and then back into base ten, you get '74 111 104 110', or '1,248,815,214' without letter spacing.
Some people actually get in trouble for copying distribution codes (in binary) and converting them into regular letters in order to redistribute them–– so technically, they're illegal!!!
2^x binary codes can be made x bits (binary digits) long, because there are two digit options per bit.
There are 3 main bases in the number system: binary (base 2), decimal (base 10), and hexadecimal (base 16). Hexadecimal is used to express binary numbers up to 4 bits long.
HEXADECIMAL DRUM SET–– http://www.mathsisfun.com/games/hex-drums.html
Math is Fun is a cool website to find stuff like this on
Sorry about subscribing issues, I'll try to fix that. Thanks to my sole follower, Ben K., for finding a way around that. See ya.
Stay coolio,
John
Friday, February 7
Venn Diagrams and Set Theory
I was researching Set Theory last night, and after thinking a little bit, I realized that geometric numbers could be used to represent items in a set. I was trying to figure out if you could make a Venn-type diagram to represent all of the subsets as equal areas. I figured out 4 sets...
but I couldn't find out what the pattern was until later. Let's say you are making a Venn-type diagram out of X sets. There would have to be all possible intersections included, or 2^X different areas. So, if 2^X is any kind of geometric number, then it can be constructed from that (regular?) geometric shape. Just a little theory...
Set theory is like the coolest thing ever. It's like all of logic in one tiny part of math. It's important for probability, exponents, and number theory, of other things. It's the idea that we can group everything, rearrange, them, and still have the same thing. How cool is that?
The most basic functions of sets are complements (what isn't in a set), unions (the combination of sets), intersections (what two sets have in common), and if (or if and only if) statements. Combining functions and sets, you can separate out any part.

That's pretty cool.
STay coolio,
John
but I couldn't find out what the pattern was until later. Let's say you are making a Venn-type diagram out of X sets. There would have to be all possible intersections included, or 2^X different areas. So, if 2^X is any kind of geometric number, then it can be constructed from that (regular?) geometric shape. Just a little theory...
Set theory is like the coolest thing ever. It's like all of logic in one tiny part of math. It's important for probability, exponents, and number theory, of other things. It's the idea that we can group everything, rearrange, them, and still have the same thing. How cool is that?
The most basic functions of sets are complements (what isn't in a set), unions (the combination of sets), intersections (what two sets have in common), and if (or if and only if) statements. Combining functions and sets, you can separate out any part.
That's pretty cool.
STay coolio,
John
Thursday, February 6
Problems of the Week
Here's some cool problems that I saw.
~~~~~~~~~~~~~~~
In a square multiplication table with the numbers 1 through 9, what is the sum of all of the products within the table?
If you think about it, the sum of each column x is 1x+2x+3x+4x+5x+6x+7x+8x+9x. All of the columns are numbered 1 through 9, so by distributive property, the sum of all the numbers is
(1+2+3+4+5+6+7+8+9)*(1+2+3+4+5+6+7+8+9), or 2025. Just a cool thought.
In some languages, every consonant must be followed by a vowel. How many words can be made from the letters in the Hawaiian word 'MAKAALA' if every consonant must be followed by a vowel?
If you think about it, the letters can be separated into four separate units 'MA', 'KA', 'LA', and 'A' because each consonant must be followed by an A. You can arrange the units in 4!=24 different ways.
Let set S be the set of all positive integers that have a remainder of 12 when divided into 192. What is the median of the set?
There are two rules to the set––
1. S must be greater than 12, by definition.
2. S be a factor of 180 (because 192-12=180).
If you write out the union of the two sets above, you find the median is 36. Just simple set theory.
There are two sticks of lengths A and B, where B is greater than A. To make a triangle from these two sticks and one extra stick, the extra stick must be strictly between 8 cm and 26 cm long. What is the area of a rectangle with side lengths A and B?
This is a cool one for its geometric properties. By definition, any one of a triangle's sides can be no longer than the sum of the other sides. So, we can work it down to––
A+B<26 and B<A+8
and from solving, A and B are 9 and 17, respectively.
~~~~~~~~~~~~~~~
We should make that a thing, where I tell you a bunch of cool problems and stuff! Fun math is the best kind of math.
Stay coolio,
John
PS.–– NEXT UP: SET THEORY!!!!!
~~~~~~~~~~~~~~~
In a square multiplication table with the numbers 1 through 9, what is the sum of all of the products within the table?
If you think about it, the sum of each column x is 1x+2x+3x+4x+5x+6x+7x+8x+9x. All of the columns are numbered 1 through 9, so by distributive property, the sum of all the numbers is
(1+2+3+4+5+6+7+8+9)*(1+2+3+4+5+6+7+8+9), or 2025. Just a cool thought.
In some languages, every consonant must be followed by a vowel. How many words can be made from the letters in the Hawaiian word 'MAKAALA' if every consonant must be followed by a vowel?
If you think about it, the letters can be separated into four separate units 'MA', 'KA', 'LA', and 'A' because each consonant must be followed by an A. You can arrange the units in 4!=24 different ways.
Let set S be the set of all positive integers that have a remainder of 12 when divided into 192. What is the median of the set?
There are two rules to the set––
1. S must be greater than 12, by definition.
2. S be a factor of 180 (because 192-12=180).
If you write out the union of the two sets above, you find the median is 36. Just simple set theory.
There are two sticks of lengths A and B, where B is greater than A. To make a triangle from these two sticks and one extra stick, the extra stick must be strictly between 8 cm and 26 cm long. What is the area of a rectangle with side lengths A and B?
This is a cool one for its geometric properties. By definition, any one of a triangle's sides can be no longer than the sum of the other sides. So, we can work it down to––
A+B<26 and B<A+8
and from solving, A and B are 9 and 17, respectively.
~~~~~~~~~~~~~~~
We should make that a thing, where I tell you a bunch of cool problems and stuff! Fun math is the best kind of math.
Stay coolio,
John
PS.–– NEXT UP: SET THEORY!!!!!
Wednesday, February 5
Golden Ratio
The Golden Ratio is equal to (1 + sqrt(5))/2. Here are some interesting properties of the Golden Ratio.
If you took a rectangle bounded by the Golden Ratio (meaning, with sides 1.61803...x and x where x is not zero) and cut the biggest square you could make off of it, you'd get a rectangle similar to the original. Basically,
1.618... : 1 = 1 : (1.618... - 1)
Artwork that incorporates the Golden Ratio in its dimensions is known to be 'visually pleasing'.
The inverse of the Golden Ratio is equal to the difference between it and one. The inverse is also equal to is conjugate.
Let's say the Fibonacci sequence is represented by F(x).
F(infinity) / F(infinity-1) = 1.618...
Also,
If you took a rectangle bounded by the Golden Ratio (meaning, with sides 1.61803...x and x where x is not zero) and cut the biggest square you could make off of it, you'd get a rectangle similar to the original. Basically,
1.618... : 1 = 1 : (1.618... - 1)
Artwork that incorporates the Golden Ratio in its dimensions is known to be 'visually pleasing'.
The inverse of the Golden Ratio is equal to the difference between it and one. The inverse is also equal to is conjugate.
Let's say the Fibonacci sequence is represented by F(x).
F(infinity) / F(infinity-1) = 1.618...
Also,
Which I thought was pretty darn cool.
The Golden Ratio is used by many plants to get more sunlight, as the angle it forms spreads out the most easily.
The Golden Ratio is a root of some simple quadratic functions, like x^2-x-1.
Just thought that was cool.
Stay coolio,
John
Thursday, January 30
Pascal's Triangle
The formula for the sum of row x in Pascal's Triangle is 2^x, and the value of each position y across in that row is xCy.
Every row beginning with a prime has only multiples of that prime in the row.
If you go down diagonally from each one in a sort-of 'knight's pattern', like in chess, and add up the numbers, you get the Fibonacci sequence.
The diagonals from the ones in the third row have triangular numbers, and if you add each adjacent one, you get square numbers.
If every odd number is colored in in an infinitely big Pascal's Triangle, you get Sierpinski's Triangle.
The contents of each row are powers of 11, with some of the contents smushed up and added together.
Stay coolio,
John
Every row beginning with a prime has only multiples of that prime in the row.
If you go down diagonally from each one in a sort-of 'knight's pattern', like in chess, and add up the numbers, you get the Fibonacci sequence.
The diagonals from the ones in the third row have triangular numbers, and if you add each adjacent one, you get square numbers.
If every odd number is colored in in an infinitely big Pascal's Triangle, you get Sierpinski's Triangle.
The contents of each row are powers of 11, with some of the contents smushed up and added together.
Stay coolio,
John
Fractal Maker
I made an amazing fractal today! I name it....
THE Z FRACTAL!!!!!!!!
Just an update, you know.
Stay coolio, John
THE Z FRACTAL!!!!!!!!
You make it by taking a line, adding lines to the end to make a Z, and repeating it with the lines you added, and et cetera. You can do it as long as the interior and exterior angles are each the same.
If the Z has base length 3 and diagonal length 5, then the formula for the entire length of the fractal is
Sorry it's scratchy. I just took a partial screenshot from Wolfram-Alpha.
By the way, the best fractal maker that I found for the Mac is @
http://www.shodor.org/master/fractal/software/Snowflake.html
It's great for experimenting and other stuff. You can change the number of segments in the first iteration, the beginning of the fractal, and the configurations. You can see the fractal up to the eighth iteration–– that's pretty good, if you ask me.
Just an update, you know.
Stay coolio, John
Subscribe to:
Comments (Atom)